Angas Tutoring
STEM Education
Your Javascript is disabled. Some navigation on this site will not work without Javascript. Please enable Javascript in your browser to enjoy all features of this site.
Home About Us Subjects Tutored FAQ Testimonials Ponder This Contact Us
Algebra Challenge Geometry Challenge Calculus Challenge Physics I Challenge

Everything should be made as simple as possible, but not simpler.
Albert Einstein
Albert Einstein

Geometry Challenge
1. Difficulty: Beginner 
Angles A and B are complementary and the measure of angle A is four times the measure of angle B. Find the measure of angle A.
Angles A and B are complementary and the measure of angle A is four times the measure of angle B. Find the measure of angle A.
72 degrees
2. Difficulty: Beginner 
In a triangle ABC the measure of angle A is 2x degrees, the measure of angle B is 3x degrees, and the measure of angle C is 4x-9 degrees. Find the measure of angle C.
In a triangle ABC the measure of angle A is 2x degrees, the measure of angle B is 3x degrees, and the measure of angle C is 4x-9 degrees. Find the measure of angle C.
75 degrees

3. Difficulty: Beginner 
In a triangle ABC the measure of angle A is 30 degrees. The measures of sides BC and AC are 2cm and 3cm respectively. Find the measure of angle B.
In a triangle ABC the measure of angle A is 30 degrees. The measures of sides BC and AC are 2cm and 3cm respectively. Find the measure of angle B.
48.6 degrees
4. Difficulty: Beginner 
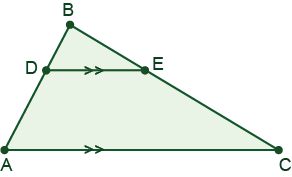
The length of the side AC in a triangle ABC is 6 cm. Points D and E lie on sides AB and BC correspondingly. Segment DE is parallel to AC and the length of segment AD is twice that of segment DB. Find the length of segment DE.
The length of the side AC in a triangle ABC is 6 cm. Points D and E lie on sides AB and BC correspondingly. Segment DE is parallel to AC and the length of segment AD is twice that of segment DB. Find the length of segment DE.
2cm
5. Difficulty: Beginner 
Find the area of the isosceles right triangle with the hypotenuse measuring 4cm.
Find the area of the isosceles right triangle with the hypotenuse measuring 4cm.
8 square centimeters
6. Difficulty: Easy 
Three points in the plane are given, not all on the same straight line. How many lines can be drawn which are equidistant from these points?
Three points in the plane are given, not all on the same straight line. How many lines can be drawn which are equidistant from these points?
3
7. Difficulty: Easy 
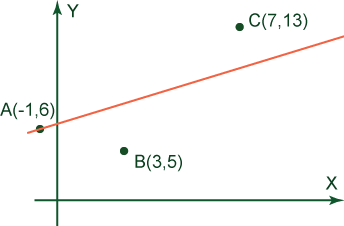
Three points on the plane are given: A(-1,6), B(3,5), and C(7,13). Find an equation of the line passing through point A that is equidistant from points B and C.
Three points on the plane are given: A(-1,6), B(3,5), and C(7,13). Find an equation of the line passing through point A that is equidistant from points B and C.
Y = 0.5X + 13/2
8. Difficulty: Easy 
In a triangle ABC the length of the side AB is 4cm and the length of the side AC is 6cm. The measure of the angle A is 60 degrees. Find the length of the segment joining the midpoints of the sides AB and AC.
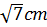
In a triangle ABC the length of the side AB is 4cm and the length of the side AC is 6cm. The measure of the angle A is 60 degrees. Find the length of the segment joining the midpoints of the sides AB and AC.
9. Difficulty: Easy 
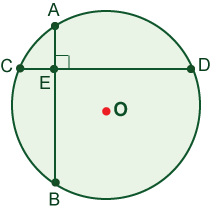
In circle O, perpendicular chords AB and CD intersect at point E so that AE = 2cm, EB = 12cm, and CE = 4cm. Find the measure of the segment ED.
In circle O, perpendicular chords AB and CD intersect at point E so that AE = 2cm, EB = 12cm, and CE = 4cm. Find the measure of the segment ED.
6cm
10. Difficulty: Medium 
In circle O, perpendicular chords AB and CD intersect at point E so that AE = 2cm, EB = 12cm, and CE = 4cm (see the previous problem). Find the measure of the radius of circle O.
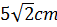
In circle O, perpendicular chords AB and CD intersect at point E so that AE = 2cm, EB = 12cm, and CE = 4cm (see the previous problem). Find the measure of the radius of circle O.
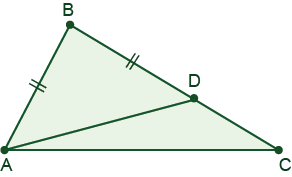
11. Difficulty: Medium 
In a triangle ABC, a point D lies on the side BC so that AB=BD. The measure of the angle BAC is 50 degrees larger than that of the angle BCA. Find the measure of the angle CAD.
In a triangle ABC, a point D lies on the side BC so that AB=BD. The measure of the angle BAC is 50 degrees larger than that of the angle BCA. Find the measure of the angle CAD.
25 degrees.
12. Difficulty: Medium 
The length of the longer base of a trapezoid is 54cm. The length of the line segment joining the midpoints of the diagonals is 5cm. Find the length of the shorter base of a trapezoid.
The length of the longer base of a trapezoid is 54cm. The length of the line segment joining the midpoints of the diagonals is 5cm. Find the length of the shorter base of a trapezoid.
44cm
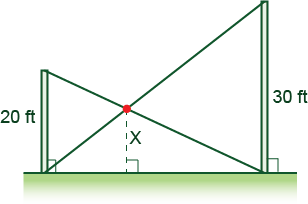
13. Difficulty: Medium 
Two telephone poles, 30 feet and 20 feet high, respectively, are placed near each other. As partial support, a line runs from the top of each pole to the bottom of the other. How high above the ground is the point of intersection of the two support lines?
Two telephone poles, 30 feet and 20 feet high, respectively, are placed near each other. As partial support, a line runs from the top of each pole to the bottom of the other. How high above the ground is the point of intersection of the two support lines?
12 feet
14. Difficulty: Medium 
The lengths of the sides of a right triangle are 60cm, 80cm, and 100cm. Find the length of a line segment, drawn from the vertex of the right angle to the hypotenuse, that divides the triangle into two triangles of equal perimeters.
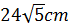
The lengths of the sides of a right triangle are 60cm, 80cm, and 100cm. Find the length of a line segment, drawn from the vertex of the right angle to the hypotenuse, that divides the triangle into two triangles of equal perimeters.
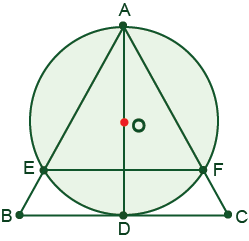
15. Difficulty: Medium 
Altitude AD of equilateral triangle ABC is the diameter of circle O. If the circle intersects sides AB and AC at points E and F, respectively, find the ratio of EF:BC.
Altitude AD of equilateral triangle ABC is the diameter of circle O. If the circle intersects sides AB and AC at points E and F, respectively, find the ratio of EF:BC.
3 : 4
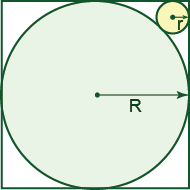
16. Difficulty: Medium 
A circle with radius R=3cm is inscribed in a square. Find the radius r of the circle that is inscribed between two sides of the square and the original circle.
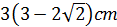
A circle with radius R=3cm is inscribed in a square. Find the radius r of the circle that is inscribed between two sides of the square and the original circle.
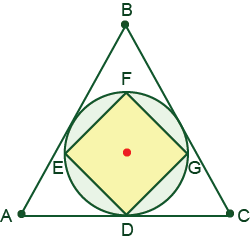
17. Difficulty: Medium 
Find the ratio between the area of a square inscribed in a circle, and an equilateral triangle circumscribed about the same circle.
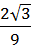
Find the ratio between the area of a square inscribed in a circle, and an equilateral triangle circumscribed about the same circle.
18. Difficulty: Medium 
In the triangle ABC, AB=8cm, AC=9cm, and BC=12cm. Points D and E are taken on segments AB and AC, respectively, so that AD=AE. If the area of the triangle ADE is ½ of the area of triangle ABC, find the length of AD.
In the triangle ABC, AB=8cm, AC=9cm, and BC=12cm. Points D and E are taken on segments AB and AC, respectively, so that AD=AE. If the area of the triangle ADE is ½ of the area of triangle ABC, find the length of AD.
6cm
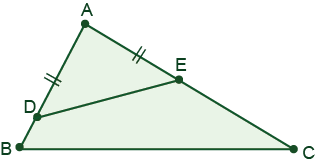
19. Difficulty: Hard 
In a triangle ABC the measure of the angle BAC is 120 degrees. Segment AD is the internal bisector of the angle BAC (point D lies on the side BC). Express the length of the segment AD in terms of the lengths of adjacent sides AB and AC.
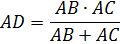
In a triangle ABC the measure of the angle BAC is 120 degrees. Segment AD is the internal bisector of the angle BAC (point D lies on the side BC). Express the length of the segment AD in terms of the lengths of adjacent sides AB and AC.
20. Difficulty: Hard 
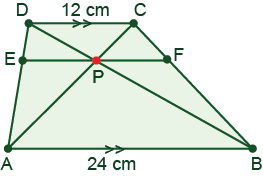
Line segments AB and CD are the bases in the trapezoid ABCD and have lengths of 24cm and 12cm respectively. The diagonals AC and DB intersect at point P. Find the length of the segment EF passing through point P and parallel to the bases with its endpoints on the legs of the trapezoid.
Line segments AB and CD are the bases in the trapezoid ABCD and have lengths of 24cm and 12cm respectively. The diagonals AC and DB intersect at point P. Find the length of the segment EF passing through point P and parallel to the bases with its endpoints on the legs of the trapezoid.
16cm
21. Difficulty: Hard 
Prove that the sum of the squares of the measures of the segments made by two perpendicular chords is equal to the square of the measure of the diameter of the given circle.
Prove that the sum of the squares of the measures of the segments made by two perpendicular chords is equal to the square of the measure of the diameter of the given circle.
22. Difficulty: Hard 
Two circles are inscribed into a larger circle so that their common internal tangent line intersects the larger circle at points A and B (see the figure). The measure of the chord AB is 6 cm. Find the area of the shaded region.
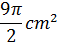
Two circles are inscribed into a larger circle so that their common internal tangent line intersects the larger circle at points A and B (see the figure). The measure of the chord AB is 6 cm. Find the area of the shaded region.
23. Difficulty: Hard 
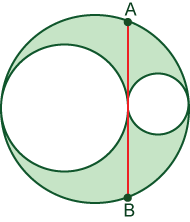
Find the area of a triangle whose medians have lengths of 21 cm, 45cm, and 60 cm.
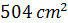
Find the area of a triangle whose medians have lengths of 21 cm, 45cm, and 60 cm.
24. Difficulty: Hard 
A circle is inscribed in a triangle whose sides are 10cm, 10cm, and 12cm in length. A second, smaller circle is inscribed tangent to the first circle and to the equal sides of the triangle. Find the measure of the radius of the second (smaller) circle.
A circle is inscribed in a triangle whose sides are 10cm, 10cm, and 12cm in length. A second, smaller circle is inscribed tangent to the first circle and to the equal sides of the triangle. Find the measure of the radius of the second (smaller) circle.
0.75cm
25. Difficulty: Hard 
Prove that from any point inside an equilateral triangle, the sum of the measures of the distances to the sides of the triangle is constant. Find this sum for the equilateral triangle with side lengths of 8cm.
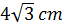
Prove that from any point inside an equilateral triangle, the sum of the measures of the distances to the sides of the triangle is constant. Find this sum for the equilateral triangle with side lengths of 8cm.
26. Difficulty: Expert 
Line segments PA andPC are tangent to the circle, and line PBD is a secant (see the figure). Chords AB, BC, CD, and DA are drawn. If AB =5cm, CD = 4cm, and DA = 8cm, find BC.
Line segments PA and
2.5cm
27. Difficulty: Expert 
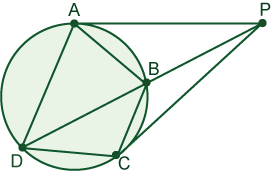
In a triangle ABC the measures of sides AB, BC, and AC are 13 cm, 4 cm, and 15 cm respectively. A semicircle is inscribed into this triangle so that its diameter lies on the side AC (see the figure). Find the radius of the inscribed semicircle.
In a triangle ABC the measures of sides AB, BC, and AC are 13 cm, 4 cm, and 15 cm respectively. A semicircle is inscribed into this triangle so that its diameter lies on the side AC (see the figure). Find the radius of the inscribed semicircle.
48/17 cm
28. Difficulty: Expert 
Find the area of a square ABCD containing a point P such that PA=3, PB=7, and PD=5.
Find the area of a square ABCD containing a point P such that PA=3, PB=7, and PD=5.
58
29. Difficulty: Expert 
Two circles, each of which passes through the center of the other, intersect at points M and N. A line from point M intersects the circles at points K and L. If the measure of KL is 5cm find the measures of LN and KN.
Two circles, each of which passes through the center of the other, intersect at points M and N. A line from point M intersects the circles at points K and L. If the measure of KL is 5cm find the measures of LN and KN.
LN = KN = 5cm
30. Difficulty: Expert 
Find the area of a triangle formed by joining the midpoints of the sides of a triangle whose medians have measures 15, 15, and 18.
Find the area of a triangle formed by joining the midpoints of the sides of a triangle whose medians have measures 15, 15, and 18.
36
31. Difficulty: Expert 
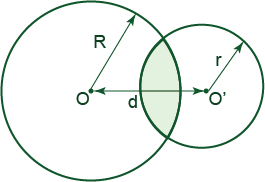
The distance between the centers of two overlapping circles of radii R and r is d ( d < R + r). Find the area of the overlap (in terms of R, r, and d ).
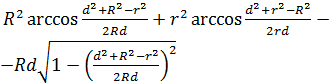
The distance between the centers of two overlapping circles of radii R and r is d ( d < R + r). Find the area of the overlap (in terms of R, r, and d ).
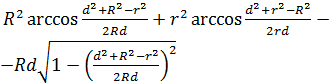
32. Difficulty: Expert 
A triangle has sides that measure 13, 14, and 15. A line perpendicular to the side of measure 14 divides the interior of the triangle into two regions of equal area. Find the measure of the segment of this perpendicular line that lies within the triangle.
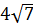
A triangle has sides that measure 13, 14, and 15. A line perpendicular to the side of measure 14 divides the interior of the triangle into two regions of equal area. Find the measure of the segment of this perpendicular line that lies within the triangle.
33. Difficulty: Expert 
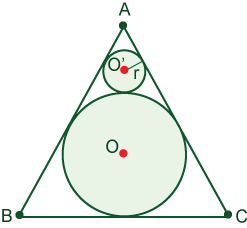
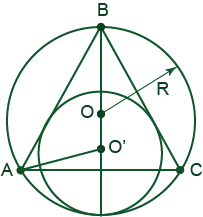
Equilateral triangle ABC is inscribed into the circle with the center O and radius R. Another circle with the center O’ is tangent to the sides AB and BC of the triangle, and to the circle O. Find the measure of the segment AO’ (in terms of radius R).
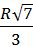
Equilateral triangle ABC is inscribed into the circle with the center O and radius R. Another circle with the center O’ is tangent to the sides AB and BC of the triangle, and to the circle O. Find the measure of the segment AO’ (in terms of radius R).
34. Difficulty: Expert 
Prove that in an isosceles triangle, the sum of the distances from any point on the base to the two other sides is fixed (constant).
Prove that in an isosceles triangle, the sum of the distances from any point on the base to the two other sides is fixed (constant).
35. Difficulty: Expert 
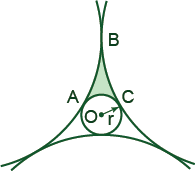
A circle with radius r is tangent to 3 larger congruent circles such that each of these larger circles is also tangent to the two other ones (see the figure). Find the area of the shaded region ABC (in terms of r).
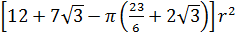
A circle with radius r is tangent to 3 larger congruent circles such that each of these larger circles is also tangent to the two other ones (see the figure). Find the area of the shaded region ABC (in terms of r).
36. Difficulty: Expert 
Two intersecting lines are given on the plane. Find the locus of points A such that the sum of the distances from A to each line is equal to a given value h.

Two intersecting lines are given on the plane. Find the locus of points A such that the sum of the distances from A to each line is equal to a given value h.

37. Difficulty: Expert 
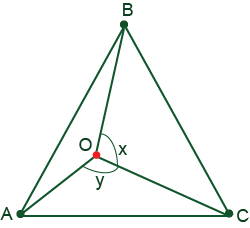
Point O is located inside an equilateral triangle ABC. The measures of the angles BOC and AOC are x and y degrees, respectively. Find, in terms of x and y, the angles of the triangle with sides measures equal to AO, BO, and CO.
Point O is located inside an equilateral triangle ABC. The measures of the angles BOC and AOC are x and y degrees, respectively. Find, in terms of x and y, the angles of the triangle with sides measures equal to AO, BO, and CO.
y-60 degrees
x-60 degrees
300 – x – y degrees
x-60 degrees
300 – x – y degrees
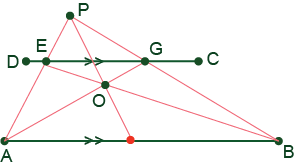
38. Difficulty: Expert 
ou are given two parallel segments AB and DC. Using only a straightedge, divide segment AB into two equal parts.
ou are given two parallel segments AB and DC. Using only a straightedge, divide segment AB into two equal parts.
Chose any two points E and G on the segment DC (could be points D and C or any other points on the segment). Draw lines AE and BG. Let’s call the intersection of lines AE and BG a point P. Draw diagonals in the trapezoid ABGE. The diagonals intersect at point O. Draw line PO. The intersection of the line PO and the segment AB is the midpoint of the segment AB.

39. Difficulty: Expert 
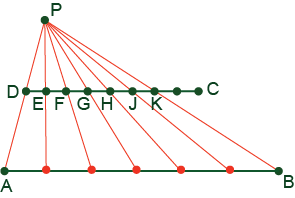
You are given two parallel segments AB and DC (see the previous problem). Using only a straightedge, divide segment AB into six equal parts.
You are given two parallel segments AB and DC (see the previous problem). Using only a straightedge, divide segment AB into six equal parts.
Using method described in the previous problem, divide segment DC into 8 equal parts – first divide it into 2 equal parts then divide each part again etc… Pick 6 equal parts consecutively, say DE, EF, FG, GH, HJ, JK. Then perform homothety mapping their union onto other segment - - i.e. draw lines AD and BK, find their intersection (point P) and draw another 5 lines: PE, PF, PG, PH, and PJ. Intersections of these lines with segment AB divide that segment into 6 equal parts.

40. Difficulty: Expert 
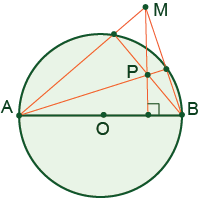
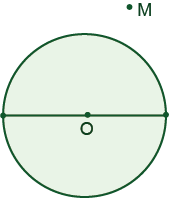
There is a circle in the plane with a drawn diameter. Given a point M outside the circle, draw the perpendicular from the point M to the diameter using only a straightedge.
There is a circle in the plane with a drawn diameter. Given a point M outside the circle, draw the perpendicular from the point M to the diameter using only a straightedge.
The height passes through point P - orthocenter of the triangle ABM, see the figure.

© Copyright Angas Tutoring. All Rights Reserved.